 Information Resource Guide |
 Information Resource Guide |
Cryptography is the science of securing data. It addresses four major concerns—confidentiality, authentication, integrity and non-repudiation. Encryption is the transformation of data into an unreadable form, using an encryption/decryption key. Encryption ensures privacy and confidentiality, keeping information hidden from anyone for whom it is not intended including those who can see the encrypted data.
A cryptosystem obeys a methodology (procedure). It includes: one or more encryption algorithms (mathematical formulae); keys used with the encryption algorithms; a key management system; plain text (the original text); and, ciphertext (the original text that has been obscured).
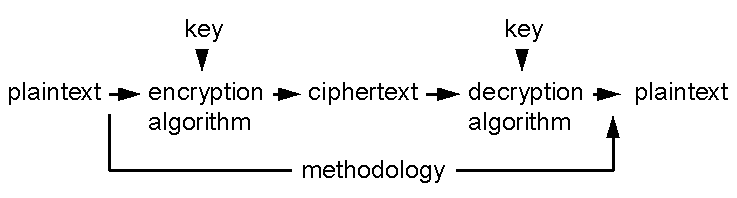
The methodology first applies the encryption algorithm and key to the plaintext to produce ciphertext. The ciphertext is transmitted to a destination where the same algorithm is used to decrypt it to produce the plaintext. The procedure (included in the methodology) to support key creation and distribution is not shown in the diagram.
In this methodology, the encryption algorithm combines with a key and plaintext to create ciphertext. The security of a strong key-based system resides with the secrecy of the key used with the encryption algorithm rather than the supposed secrecy of the algorithm. Many encryption algorithms are publicly available and have been well tested (e.g. Data Encryption Standard).
However, the main problem with any key-based methodology is how to create and move the keys securely among communicating parties. How does one establish a secure channel between the parties prior to transmitting keys?
Another problem is authentication. There are two potential areas of concern here:
| TERM | MEANING | POTENTIAL CONFUSION |
| Symmetric methodology | Uses one key
which both encrypts and decrypts using the same symmetric encryption algorithm
The key is distributed to the two communicating parties in a secure manner prior to transfer of encrypted data |
Often called private or private-key methodology |
| Asymmetric methodology | Uses symmetric
encryption algorithms and symmetric keys to encrypt data
Uses asymmetric encryption algorithms and asymmetric keys to encrypt the symmetric key. The two keys are created and are linked together. The symmetric key encrypted with one must be decrypted by the other (in either direction) using the same asymmetric encryption algorithm. The two linked asymmetric keys are created together. One must be distributed to the owner, and the other to the party which is keeping these keys (often called the CA) in a secure manner prior to transfer of data |
Often called public or public-key methodology |
| Private key (1) | Symmetric methodology | Uses a single key which can both encrypt and decrypt. See above. |
| Private key (2) | Symmetric (private) encryption key | Symmetric private key |
| Private key (3) | Asymmetric private encryption key | Asymmetric
private key
Asymmetric keys are created as pairs that are linked together. The words private key often mean the half of the asymmetric key pair that is kept private. The asymmetric private key is a totally different thing from the symmetric private key. |
| Public key (1) | Asymmetric methodology | Uses a pair of keys, both of which are created together and are linked. Anything encrypted by one must be decrypted by the other. |
| Public key (2) | Asymmetric (public) encryption key | Asymmetric
keys are created as pairs that are linked together.
The words public key often mean the half of the asymmetric key pair which is made publicly available. |
| Session key | Symmetric (private) encryption key | Used by asymmetric
methodology for the actual data encryption of data using symmetric methodologies
Simply a symmetric private key (see above) |
| Encryption algorithm | Mathematical formula | Symmetric keys
are required for symmetric algorithms
Asymmetric keys are required for asymmetric algorithms You cannot use symmetric keys with asymmetric algorithms, and vice versa |
| Private cryptosystems | Use symmetric algorithms and symmetric (private) keys to encrypt data | Used by symmetric (private) cryptosystems |
| Public cryptosystems | Use asymmetric
algorithms and asymmetric keys to encrypt session keys
uses symmetric algorithms and symmetric keys to encrypt data |
Used by asymmetric (public) cryptosystems only |
| Public/private | Many asymmetric cryptosystem vendors define their methodologies as public/private | Usually not clarified that asymmetric methodologies use symmetric methodologies to actually encrypt data |
6.1.1 Symmetric (Private) Methodology
In this methodology, both encryption and decryption operations use the same key with the sender and receiver agreeing on the key before they can communicate. Provided the keys have not been compromised, authentication is implicitly resolved because only the sender has a key capable of encrypting and only the receiver has the same key capable of decrypting. Because the sender and the receiver are the only people who know this symmetric key, if the key is compromised, only these two users’ communication is compromised. The problem, which is the same for all types of cryptosystems, is how to distribute the symmetric (private) key securely.
Symmetric key encryption algorithms use small-length keys and can quickly encrypt large quantities of data.
The process involved with symmetric key systems is:
Here, the encryption and decryption keys are different from each other, although they are produced together. One key is made public; the other key is kept private. While both keys can encrypt and decrypt, data encrypted by one can only be decrypted by the other.
All asymmetric cryptosystems are subject to shortcut attacks as well as brute force, and therefore, must use much larger keys than symmetric cryptosystems to provide equivalent levels of security. This immediately impacts computing cost, although using elliptic curve algorithms may reduce this problem. Bruce Schneier in his book "Applied Cryptography: Protocols, Algorithms, and Source Code in C" provides the following table comparing equivalent key lengths:
| SYMMETRIC KEY LENGTH | PUBLIC-KEY KEY LENGTH |
| 56 bits | 384 bits |
| 64 bits | 512 bits |
| 80 bits | 768 bits |
| 112 bits | 1792 bits |
| 128 bits | 2304 bits |
In order to circumvent the slowness of the asymmetric encryption algorithms, a temporary, random, small, symmetric session key is generated for each message and is the only part encrypted by the asymmetric algorithm. The message itself is encrypted using this session key and an encryption/decryption algorithm. The small session key is then encrypted using the sender’s asymmetric private key and encryption/decryption algorithm. This encrypted session key along with the encrypted message is then transmitted to the receiver. The receiver uses the same asymmetric algorithm and the sender’s asymmetric public key to decrypt the session key, and the recovered plaintext session key is used to finally decrypt the message.
It is important in asymmetric cryptosystems that the session and asymmetric keys must be comparable in terms of the security they produce. If a short session key is used (e.g. 40 bit DES), it does not matter how large the asymmetric keys are. Hackers will attack the session key instead. The asymmetric public keys are susceptible to brute-force attacks partly because it is difficult to change them. Once broken, all current and future communication is compromised, often without anyone knowing.
The process involved with asymmetric-key systems is:
It is obvious that both types of cryptosystems have a problem distributing the keys.
Symmetric methodologies squarely face up to this fact and define how keys are to be moved between the parties before communication can take place. How this is done depends upon the security required. For lower security requirements, sending keys by a delivery mechanism of some kind (such as postal mail or a parcel delivery service) may be adequate. Banks use the postal service to deliver PINs, which are, in essence, easily crackable symmetric keys that may or may not unlock other keys, or your money! Very high security requirements may require hand delivery of keys, possibly in parts by several people.
Asymmetric methodologies try to get around the problem by encrypting the symmetric key and attaching it to the encrypted data. They then try to make it possible to distribute the asymmetric keys used to encrypt the symmetric key by employing a CA to store the public asymmetric key. The CA in turn digitally signs the keys with the CA’s private asymmetric key. Users of the system must also have a copy of the CA’s public key. In theory, this means that the communicating parties do not need to know about each other ahead of secure communication.
Proponents of asymmetric cryptosystems maintain that this mechanism proves authenticity and is sufficient.
The problem still remains, however. The asymmetric key pair must be created together. Both keys, whether they can be made publicly available or not, must be sent securely to the owner of the key, as well as to the Certification Authority. The only way to do this is by some kind of delivery mechanism for low security requirements, and hand-delivery for high security requirements.
The problems of the asymmetric mechanism include the following:
Key management refers to the distribution,
authentication and handling of keys. No matter what kind of cryptosystem
is used, keys must be managed. Secure methods of management are very important
as many attacks on key-based cryptosystems are aimed at key management
procedures.
| PROCEDURE | COMMENTS |
| Physically distribute the keys | Couriers and
hand delivery are two examples. Of the two, hand delivery is better.
Secure organizations have written procedures surrounding key distribution Can be audited and logged, although open to compromise by individuals Used by both symmetric and asymmetric cryptosystems. In spite of claims that asymmetric cryptosystems avoid the problem of physical delivery of keys, the problem actually exists. X.509 assumes that the creator will release the asymmetric private key to the user (and/or the asymmetric public key to the CA) in a physically secure manner, and that suitable physical security measures are in place so that the creator and data operations are free from tampering. |
| Issue a common key from a central issuing authority | Could be used
by both symmetric and asymmetric cryptosystems
As each user must be able to communicate with the central authority securely in the first place, this is yet another situation where initial key exchange is a problem If the central authority is compromised, further requests for keys are at risk; keys already in place may be safe depending on the cryptosystem |
| Allow access to public keys from a centralized certification authority and provide private keys to users | Used by asymmetric
cryptosystems
Users must blindly trust the entire system A single security breach compromises the entire system Hierarchical system of attestation leads to more potential intruder entry points—a CA must publicize its asymmetric public key and provide a certificate from a higher-level CA validating it. This sets up a hierarchy of CAs. CA asymmetric private keys must be stored securely because compromise could result in undetectable forgeries |
| Web of trust | Used by asymmetric
cryptosystems
Users distribute and track each other’s keys, and trust in an informal, distributed fashion |
| Diffie-Hellman | Exchange of
a secret key over an insecure medium by two users without any prior secrets
Cannot be used to encrypt or decrypt messages Based on the difficulty of taking logarithms in finite fields. If the elements are carefully chosen, and are large, then the discrete logarithm problem is computationally infeasible. Vulnerable to man-in-the-middle attacks Patented by PKP (Public Key Partners) |
6.1.4 Encryption Ciphers or Algorithms
Key-based algorithms disguise data so that it cannot be read by anyone without a decryption key. They are divided into two classes depending on the cryptography methodology they directly support. Please read Schneier’s Applied Cryptography for a full description of the algorithms.
The same private key is used
to encrypt and decrypt. This type of algorithm is used by both symmetric
and asymmetric methodologies to encrypt data.
| TYPE | DESCRIPTION |
| DES (Data Encryption Standard) | Popular, product
cipher used by the Data Encryption Standard of the US Government
64-bit block cipher, 64-bit key (only 56 are needed), 16 rounds Operates in four modes:
|
| 3-DES or Triple DES | 64-bit block
cipher, using the DES cipher 3 times, three distinct 56-bit keys
Strong under all attacks |
| Chained 3-DES | Standard Triple-DES
with the addition of a feedback mechanism such as CBC, OFB or CFB
Very strong under all attacks |
| FEAL (Fast Encryption Algorithm) | Block cipher,
used as an alternative to DES
Broken, although new versions have been proposed |
| IDEA (International Data Encryption Algorithm) | 64-bit block
cipher, 128-bit key, 8 rounds
Recently proposed; although it has not yet received enough scrutiny for full confidence, it is considered superior to DES |
| Skipjack | Developed by
NSA as part of the US Government Clipper and Capstone projects
Classified as secret, although its strength does not depend only on the secrecy of the algorithm 64-bit block cipher, 80-bit keys used in ECB, CFB, OFB or CBC modes, 32 rounds |
| RC2 | 64-bit block
cipher, variable key sizes
Approximately twice as fast as DES Can be used in same modes as DES including triple encryption Confidential algorithm proprietary to RSA Data Security |
| RC4 | Stream cipher,
byte-oriented, variable key size
Approximately 10 times as fast as DES Confidential algorithm proprietary to RSA Data Security |
| RC5 | 32, 64 or 128-bit
variable block size, 0 to 2048 variable key size, 0 to 255 rounds
A fast block cipher Proprietary to RSA Data Security |
| CAST | 64-bit block
cipher, 40 to 64 bit keys, 8 rounds
No known way to break other than brute force Generally, the particular S-boxes used (which form the strength of the algorithm) are not made public |
| Blowfish | 64-bit block
cipher, variable, up to 448-bit key, 16 rounds, each consisting of a key-dependent
permutation and a key-and-data-dependent substitution
Faster than DES Designed for 32-bit machines |
| One-time pad | A proven unbreakable
cipher
The key (same length as the text) is the next ‘n’ bits of randomly created bits found on a pad to which both the sender and the receiver have access. As soon as the bits are used, they are destroyed and the next bits on the pad are used for the next encryption |
| Stream ciphers | Fast, symmetric
encryption algorithms, usually operating on bits (not blocks) of data
Developed as an approximation of the one-time pad which, while not as secure as the one-time pad, are at least practical |
Asymmetric algorithms are used by asymmetric cryptosystem methodologies in order to encrypt a symmetric session key (which is actually used to encrypt the data).
Two distinct keys are used—one
that is publicly available, and the other that is kept private and secret.
Usually both keys perform encryption and decryption functions. However,
data encrypted by one can only be decrypted by the companion key.
| TYPE | DESCRIPTION |
| RSA | Popular asymmetric encryption algorithm, whose security depends on the difficulty in factoring large integers |
| ECC (Elliptic Curve Cryptosystem) | Uses the algebraic
system defined on the points of an elliptic curve to provide asymmetric
cryptographic algorithms
Emerging as competition to other asymmetric algorithms because it offers equivalent security using shorter key lengths and faster performance. Current implementations indicate that these systems are far more efficient than other public-key systems. Performance figures show an order of magnitude improvement in efficiency over RSA, Diffie-Hellman and DSA. |
| ElGamal | Variant of the Diffie-Hellman which can be used for both digital signatures and encryption |
Hash functions are central to key-based
cryptosystems. They are relatively easy to compute, but almost impossible
to decrypt. A hash function takes a variable size input and returns a fixed
size string (sometimes called a Message Digest), usually 128 bits. Hash
functions are used to detect modification of a message (i.e. provides a
digital signature).
| TYPE | DESCRIPTION |
| MD2 | Slowest, optimized for 8-bit machines |
| MD4 | Fastest, optimized
for 32-bit machines
Now broken |
| MD5 | Most commonly
used of the MD functions
similar to MD4, but with added security features making it 33% slower than MD4 Provides data integrity Considered secure |
| SHA (Secure Hash Algorithm) | Produces
160-bit hash values from variable-sized input
Proposed by NIST and adopted by the US Government as a standard Designed for use with the proposed DSS (Digital Signature Standard) and part of the US Government’s Capstone project |
6.1.8 Authentication Mechanisms
These mechanisms securely and
reliably confirm identity or authenticity.
| TYPE | DESCRIPTION |
| Passwords or PINs (Personal Identification Numbers) | Something a
user knows and shares with the entity at the other end
Typically part of a two way handshake Can be exchanged in both directions to obtain mutual authentication |
| One-time password | Password provided
is never reused
Time is often used as the constantly changing value on which the password is based |
| CHAP (Challenge Handshake Authentication Protocol) | One side initiates
an authentication exchange, is presented with a unique and unpredictable
challenge value, and based on a secretly shared value, is able to calculate
and return an appropriate response
Can be used to provide user authentication as well as device authentication |
|
Callback |
Dialing in over a telephone to a server which is configured to dial back to a specified number associated with the user |
6.1.9 Digital Signatures and Time Stamps
A digital signature provides data
integrity, but does not provide confidentiality. The digital signature
is attached to the message and both can be encrypted if confidentiality
is desired. The addition of a timestamp to a digital signature provides
a limited form of non-repudiation.
| TYPE | COMMENTS |
| DSA (Digital Signature Authorization) | Public key
algorithm used for digital signatures but not for encryption
Private hashing and public verification—only one person can produce the hash for a message, but everyone can verify that the hash is correct Based on the difficulty of taking logarithms in finite fields |
| RSA | Patented RSA
digital signature proves the contents of a message as well as the identity
of the signer
The sender creates a hash of the message, and then encrypts it with the sender’s private key. The receiver uses the sender’s public key to decrypt the hash, hashes the message himself, and compares the two hashes. |
| MAC (Message Authentication Code) | Digital signature, using hashing schemes similar to MD or SHA, but the hash value is a function of both the pre-image and a private key |
| DTS (Digital Timestamp Service) | Issues timestamps which associate a date and time with a digital document in a cryptographically strong manner |
Section References
6.0 Chandler, Janet, Cryptography
101: Technical White Paper, Signal 9 Solutions, Kanata Ontario.